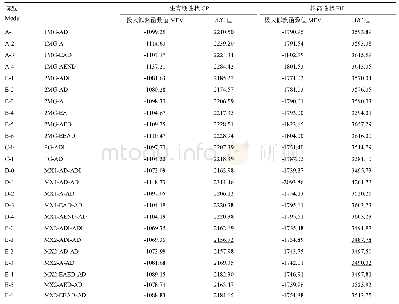
《表8 3个非多项式函数在不同方法下的逼近误差比较》

  提示：宽带有限、当前游客访问压缩模式

本系列图表出处文件名：随高清版一同展现

《光滑函数实根计算的渐进显式公式》

1. 获取 高清版本忘记账户？点击这里登录

1. 下载图表忘记账户？点击这里登录

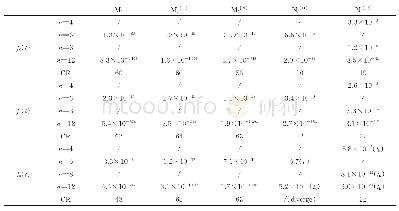
例3测试3个非多项式函数，比较渐进法M1，M2，M3和类牛顿法N2，N3。3个非多项式函数分别为f6（t）=（t-1/2）[esin（10(t-π））+4(t-π）-1]，t∈[3，3.3]，f7(t）=tanh（2t-π/25），t∈[-0.5，0.5]，f8（t）=-1/t+sin（t）+1，t∈[0.01，1.3]。其单根分别为t6*=π，t7*≈0.062 8，t8*≈0.629 446 5。由定理3知，可用一个初始值得到一个包含实根的小区间。表8所列为每步的逼近误差和收敛阶。由表8可知，对于f6（t）和f7(t），N2和N3收敛至正确结果；而对于f8（t），N2在ta=5.334 7附近发散，N3则收敛至错误解tb=16.933。3种情况下，渐进法均能收敛至正确结果。因此，渐进法M1，M2和M3的收敛阶相差不大，且均较类牛顿法N2和N3的收敛速度快得多。表9为在不同有效位数下运行12次FE的总计算时间。由表9可知，M1，N2和N3的计算效率相当，均较M2和M3好。M1在相同时间内获得最小的逼近误差，并在给定的相同误差下，计算效率最高。