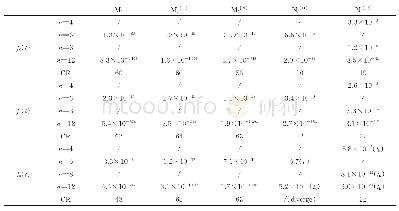
《表1 0 例4中M1在3个子区间内的逼近误差》

  提示：宽带有限、当前游客访问压缩模式

本系列图表出处文件名：随高清版一同展现

《光滑函数实根计算的渐进显式公式》

1. 获取 高清版本忘记账户？点击这里登录

1. 下载图表忘记账户？点击这里登录

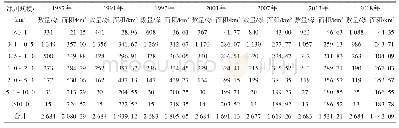
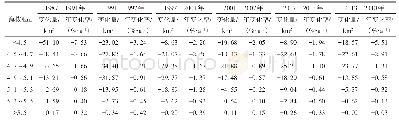
在区间[0，25]内的实根。该Wilkinson多项式有20个实根Wi，i=1，2，?，20（参见文献[15]中的例6）。首先，计算相应控制多边形的零点，即{0.27，1.55，2.83，4.11，5.38，6.65，7.92，9.19，10.46，11.73，13.007，14.27，15.54，16.81，18.07，19.34，20.61，21.87，23.14，24.40}，并将区间[0，25]划分为20个子区间，其中有16个子区间包含W（t）的1个或2个根。本文选取其中的3个子区间Λ1=[0.27，1.55]、Λ2=[2.83，4.11]、Λ3=[16.81，18.07]用以说明更多细节。此3个子区间分别包含1个、2个、2个根。可将RBM直接应用于Λ1，因为W(t）在其2个端点的函数值异号；对于Λ2和Λ3，可选择区间中点作为分界点，将每个区间拆分为2个子区间，每个子区间都包含1个根。然后，将RBM应用于子区间，由注1的方法获得优化区间。本例中，区间[0.27，1.55]、[2.83，4.11]、[16.81，18.07]对应的优化区间为Γ1=[0.99，1.0034]、Γ2=[2.83，3.004]、Γ3=[17.988，18.07]。如表10所示，在误差ei映射到重新参数化函数?i (t）的情况下，RBM的效果较好，表明用RBM处理多根情形也具有较好的计算稳定性。