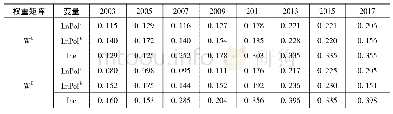
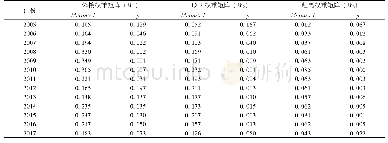
《表4 各主因子的全局Moran指数值》
利用Geoda软件以欧式距离形成空间矩阵,计算各主因子的全局Moran指数值。在0.001的显著性水平下,第1、4、5主因子的全局Moran指数显著为正,说明非劳动年龄人口、定居就业人口和居住条件均出现空间集聚,其中居住条件的集聚趋势最为突出。第2、3主因子的全局Moran指数均接近于0,说明知识分子和外来人口的空间分布基本不相关(表4)。以自然间断点法将各街道乡镇的因子得分分为五级,主要得分等级的街道组成见表5,空间分布及空间自相关分布见图2。
| 图表编号 | XD00314600 严禁用于非法目的 |
|---|---|
| 绘制时间 | 2019.11.09 |
| 作者 | 杨莹、冯健 |
| 绘制单位 | 北京大学城市与环境学院 |
| 更多格式 | 高清、无水印(增值服务) |
 提示:宽带有限、当前游客访问压缩模式
提示:宽带有限、当前游客访问压缩模式