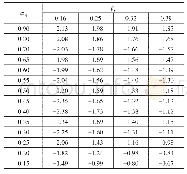
《表1 通过拟合I=1.12×1014W/cm2时x=0处量子势的振荡行为,获得电子波函数中各个态的系数(b0~b4,c)和连续态的能量E.ε0~ε4分别代表原子体系中最低5个束缚态的本征值》
接下来,我们将结合对激光场中电子波函数特性的分析,揭示在I=1.12×1014W/cm2时量子势不同寻常的振荡行为与原子共振激发效应之间的紧密联系.为了便于分析,同时更清晰地展示量子势振荡行为,图3(g)~(i)中的红线给出了x=0处量子势大小随时间的变化.在玻姆力学中,量子势与电子波函数紧密相关(方程(3)),为了理解中心区域量子势的振荡行为,分析了相应区域的电子波函数.在强激光场作用下,处于基态的电子波函数以隧穿方式到达连续态[13],然后在激光场驱动下运动,其中部分波包会返回中心区域[11,12],因此中心区域电子波函数可以近似表达为基态?0(x)和返回动量大小为p的连续态的相干叠加态:(x,t)~0(x)ei 0t+ceip xe iEt,其中E=p2/2代表返回能量,c是展开系数,这里把系数和能量引起的相位因子(ei 0t,ei Et)在波函数中分开,可以更容易地比较不同激光强度下系数的大小.由于我们关注短时间范围内中心区域量子势的变化,为了简化分析,假设返回动量p在短时间内近似不变,即能量E大小不变.接着,把电子波函数代入方程(3)拟合x=0处量子势振荡行为随时间的变化,得到待定参数c和E.如图3(g)和(i)中的黑线所示,在I=1.02×1014和1.22×1014W/cm2时,中心区域量子势的振荡行为可以定性上较好地分别用c=0.0028+0.045i和E=0.737 a.u.与c=0.088–0.0274i和E=0.879 a.u.来拟合,其中返回能量E随激光强度增大而增大,这与半经典计算结果相一致[11,12].然而,分析发现,在I=1.12×1014W/cm2时的量子势振荡行为,即峰之间的时间间隔随时间的非线性变化无法用上面的简单波函数来拟合,可能原因是在激光与原子相互作用过程中,部分电子波函数同时明显地处于某些束缚激发态?n(x)(n=1,2,3,4,…).为此,我们在电子波函数中加入束缚激发态,并按照激发态本征能量从低到高的顺序将中心区域电子波函数近似表达为,其中bn和εn(n=0,1,2,3,4)分别代表各个束缚态的系数和本征能量.把这个波函数重新代入方程(3),并借助群鸟算法[44,45]拟合x=0处量子势振荡行为随时间的变化.由于量子势只与波函数相对大小有关,令b0=1.如图3(h)中的黑线所示,理论拟合得到的量子势振荡行为定性上与从头计算结果相一致,相应的拟合系数见表1.通过仔细分析表1,我们发现第三激发态的系数|b3|远大于系数|b1|、|b2|和|b4|,表明第三激发态具有明显的分布,存在基态与第三激发态之间的共振过程,这与前人利用弗洛凯方法(Floquet)分析共振能级结果相一致[43].需要说明的是,即便在前述待定的总电子波函数中加入更多高激发态,拟合结果几乎不变,表明高激发态对量子势振荡行为影响不大.因此,我们的模拟结果表明,在光强I=1.12×1014W/cm2时,受原子共振激发影响,电子波函数分布发生变化,导致量子势不同寻常的振荡行为.
| 图表编号 | XD00204313000 严禁用于非法目的 |
|---|---|
| 绘制时间 | 2021.03.20 |
| 作者 | 赖炫扬、黄祎祎、余少刚、柳晓军 |
| 绘制单位 | 中国科学院精密测量科学与技术创新研究院波谱与原子分子物理国家重点实验室、中国科学院精密测量科学与技术创新研究院波谱与原子分子物理国家重点实验室、中国科学院精密测量科学与技术创新研究院波谱与原子分子物理国家重点实验室、中国科学院精密测量科学与技术创新研究院波谱与原子分子物理国家重点实验室 |
| 更多格式 | 高清、无水印(增值服务) |
 提示:宽带有限、当前游客访问压缩模式
提示:宽带有限、当前游客访问压缩模式