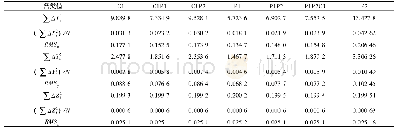
《表2 各阶导数的均方根误差Tab.2 Root mean square error of every derivative》

  提示：宽带有限、当前游客访问压缩模式

本系列图表出处文件名：随高清版一同展现

《一种获取噪声信号分数阶导数的方法》

1. 获取 高清版本忘记账户？点击这里登录

1. 下载图表忘记账户？点击这里登录

式中x=0，1，…，999。然后，叠加白噪声使其信噪比为30 dB，计算它的不同分数阶导数，结果如图2所示。文献[13]也讨论了噪声信号的分数阶导数获取问题，他们应用高斯核的分数阶导数对噪声信号进行卷积来获得噪声信号的分数阶导数，相当于用高斯平滑再求导，而本文方法是先用多项式拟合再求导，这也是一种被广泛使用的信号平滑方法[15]，由于幂函数的分数阶导数可以准确得到，结合分数阶导数的线性性质，就很容易得到窗口中数据的分数阶导数。由于信号g（t）的真实分数阶导数无法获取，作为2种方法的比较，此处采用整数阶导数进行比较，在这2种方法中，整数阶导数均是他们的特例，而且信号g（t）的整数阶导数可以准确得到，那种方法的整数阶导数的效果好其分数阶导数的效果也应该好。在文献[13]中，也要给定高斯核的窗宽，本文方法中也须给定拟合窗口的宽度，此处设定2种方法的窗口宽度一样的情况下进行比较。相应的比较结果给出于表2中，从表中可看出本文方法能得到更好的分数阶导数。此外，文献[13]中采用高斯核对噪声信号平滑，对于高阶导数需要多次卷积才能得到比较光滑的导数，而本文方法是一次性得到导数，使用更方便。