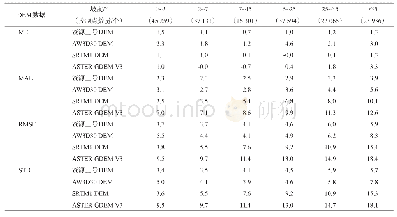
《表8 问题4当ε=0.001时,在不同网格数N下的最大绝对误差和收敛阶》
 提示:宽带有限、当前游客访问压缩模式
提示:宽带有限、当前游客访问压缩模式
本系列图表出处文件名:随高清版一同展现
《椭圆型方程两点边值问题的混合型高精度紧致差分格式》
表5~8给出了问题4当ε=1,0.1,0.01,0.001时的计算结果,注意到对于该问题当ε很小时,它的精确解在x=1处有一边界层。分别采用中心差分格式和本文格式进行了计算,由表5可以看出当ε=1时,本文BCD6格式能够达到理论上的六阶精度。伴随着ε的逐步减小,边界层变得越来越薄,只有在网格数增大到一定程度时,本文格式才可达到理论上的六阶精度。对于中心差分格式而言当ε较大时,如ε=1,0.1时可以达到理论上的二阶精度,但当ε较小时如ε=0.01,0.001,必须采用较多的网格数才可达到二阶精度。
| 图表编号 | XD00302100 严禁用于非法目的 |
|---|---|
| 绘制时间 | 2019.11.25 |
| 作者 | 马廷福、葛永斌 |
| 绘制单位 | 宁夏大学数学统计学院、宁夏大学数学统计学院 |
| 更多格式 | 高清、无水印(增值服务) |