《表2 Smith-Waterman算法性能结果》
 提示:宽带有限、当前游客访问压缩模式
提示:宽带有限、当前游客访问压缩模式
本系列图表出处文件名:随高清版一同展现
《基于FPGA的Smith-Waterman算法的加速与实现》
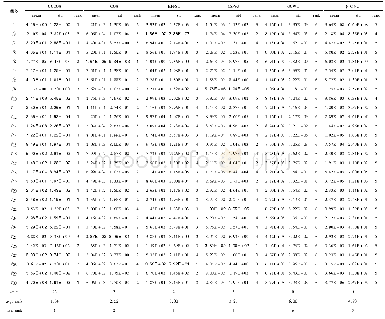
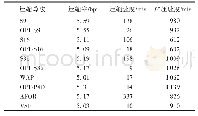
比较Smith-waterman算法性能的标准度量方法CUPS(Cell Updates Per Second)表示每秒求得的单元数目。研究者为了加速smith-waterman算法,使用了各种不同的加速平台[10]。有在CPU+GPU的异构平台上进行加速smith-waterman算法,实现的速度只有3072MCUPS.使用纯软件加速最快的版本是SSW,加速效果远不如使用FPGA。在使用FPGA作为加速平台方面,Sirasao使用Xilinx Virtex-7实现该算法速度达到135.4GCUPS。Ernst Joachim Houtgast使用BittWare A10PL4 FPGA实现该算法,速度为107.2GCUPS.使用Intel A10_REF开发板实现的速度为214.4GCUPS,为目前已知实现smith_waterman算法的最快速度。本文实现的速度为294.6G,优于目前已知的最优速度。本文在使用资源时,存在Logic和RAM使用的均衡问题,可再进行优化,用RAM来代替部分logic,更充分的利用资源,因此该方案可实现的速度会更快。为了更加充分的使用资源,把整个代码复制多份即并行模块数,并行运算提高运算速度。最大理论值的计算方法如下:理论最大值=并行模块数*频率*PE数。表一是本文实现该算法在不同并行模块数下的PE个数、频率以及FPGA资源使用情况。表2是该方案实现的速度与其他方案实现速度的对比。
| 图表编号 | XD00100672100 严禁用于非法目的 |
|---|---|
| 绘制时间 | 2019.07.20 |
| 作者 | 周智、徐渊、邓建晖、唐桐升、吴琪 |
| 绘制单位 | 深圳大学电子信息与工程学院、深圳技术大学、深圳大学电子信息与工程学院、深圳大学电子信息与工程学院、深圳大学电子信息与工程学院 |
| 更多格式 | 高清、无水印(增值服务) |